Programming Language R
Coding Exercise
Plotting binomical distribution, scatter plot, box-plot, probability distribution, and Gaussian Curve
Problem 1: Binomial Distribution
n <- 60
# for p=0.3, generating statistical summary
p <- 0.3
bin_dist_0.3 <- dbinom(0:n, n, p)
summary(bin_dist_0.3)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 0.00 0.00 0.02 0.01 0.11sd(bin_dist_0.3)
## [1] 0.03
# for p=0.5, generating statistical summary
p <- 0.5
bin_dist_0.5 <- dbinom(0:n, n, p)
summary(bin_dist_0.5)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 0.00 0.00 0.02 0.01 0.10
sd(bin_dist_0.5)
## [1] 0.03
# for p=0.8, generating statistical summary
p <- 0.8
bin_dist_0.8 <- dbinom(0:n, n, p)
summary(bin_dist_0.8)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 0.00 0.00 0.02 0.01 0.13
sd(bin_dist_0.8)
## [1] 0.04preparing for the plot
x <- seq(0,n,1)
X <- c(x,x,x)
bin_dist <- c(bin_dist_0.3,bin_dist_0.5,bin_dist_0.8)
binomial.distribution <- data.frame(X,bin_dist)
n <- as.numeric(rownames(binomial.distribution))
binomial.distribution <- binomial.distribution %>%
mutate(p = ifelse(n<61, "p=0.3", ifelse(n<122, "p=0.5", "p=0.8")))Plotting Binomial Distribution
binomial.distribution %>%
ggplot() +
geom_line(aes(x=X, y=bin_dist, col=p)) +
ggtitle("Binomial Distribution") +
ylab("")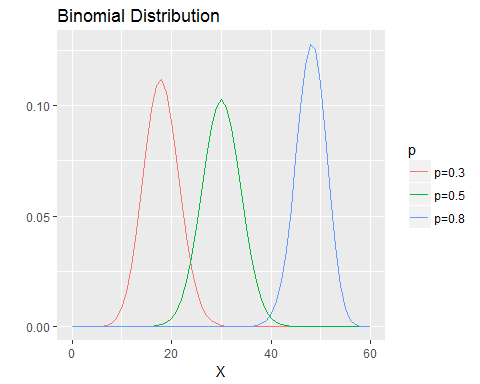
Plotting Boxplot
boxplot(bin_dist ~ p,
data = binomial.distribution,
names = c("p=0.3", "p=0.5", "p=0.8"))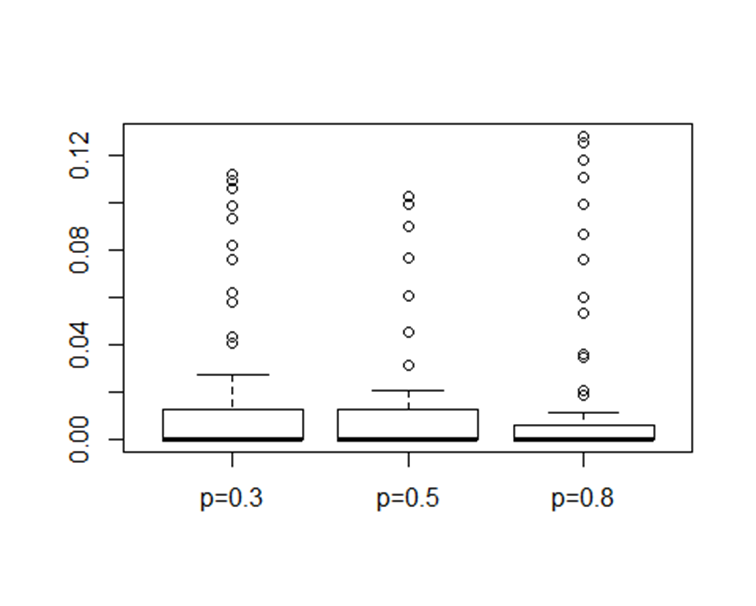
Problem 2: Relationship between waiting and duration of eruptions
Getting data
faithful.data <- as.data.frame(faithful)
attach(faithful.data)Plotting a scatter plot waiting vs. duration of eruptions
plot(x = eruptions,
y = waiting,
main = "waiting vs. duration",
xlab = "duration")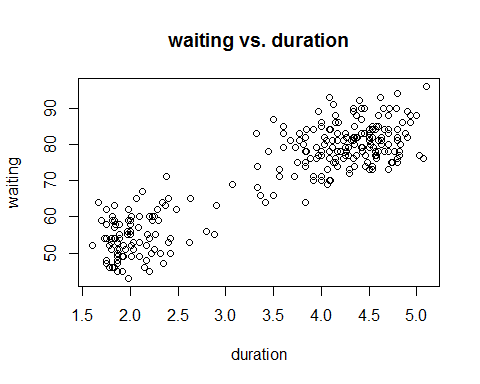
linear model fit
model <- lm(waiting ~ eruptions)
model##
## Call:
## lm(formula = waiting ~ eruptions)
##
## Coefficients:
## (Intercept) eruptions
## 33.5 10.7linear association between duration of eruptions and waiting between eruptions
plot(x = eruptions,
y = waiting,
main = "waiting vs. duration",
xlab = "duration")
abline(model,
col = "red",
lwd = 3)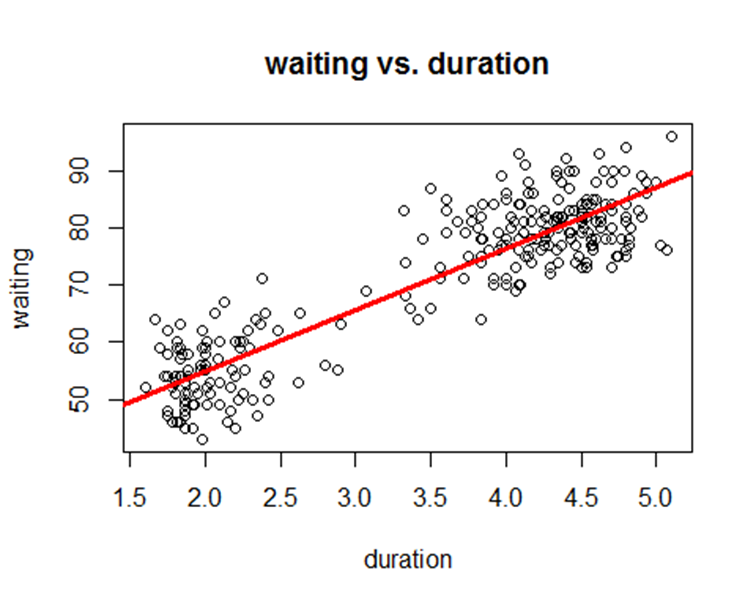
Problem 3: short vs. long eruptions
detach(faithful.data)
faithful.data <- faithful.data %>%
mutate(type = ifelse(eruptions<3.1, "short", "long" ))
boxplot(waiting ~ type,
data = faithful.data,
ylab = "waiting",
main = "Waiting between eruptions: long vs. short eruptions")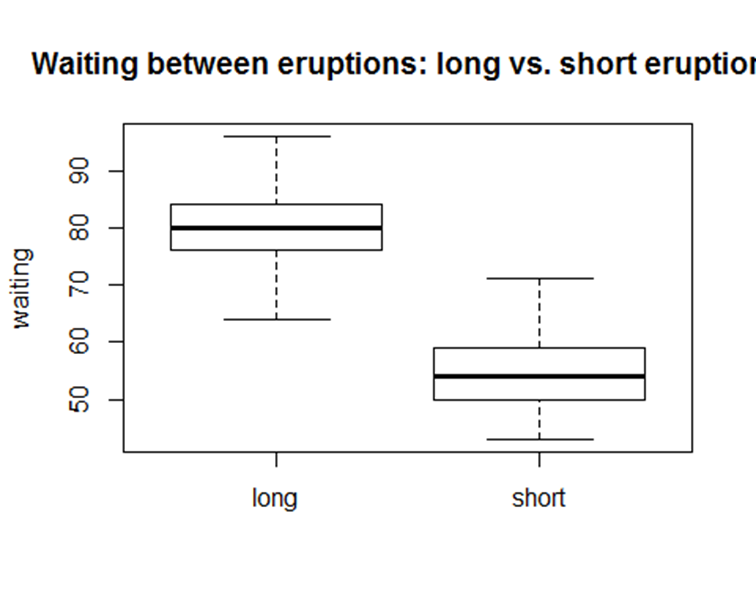
boxplot(eruptions ~ type,
data = faithful.data,
ylab = "Duration of eruptions",
main = "Duration of each eruption: long vs. short eruptions")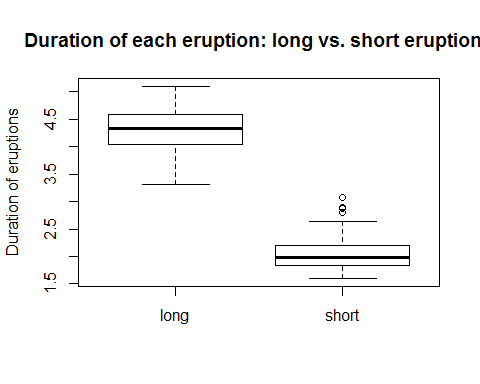
Problem 4: Uniform Probability Distribution
generating random variable which follows uniform distribution
n <- 10000
min <- -1
max <- 2
parameter <- runif(n, min = min, max = max)plotting distribution of random variable generated above
breaks <- seq(min, max, (max-min)/20)
xrange <- range(-2,3)
hist(parameter,
breaks = breaks,
right = FALSE,
col = "light blue",
xlim = xrange,
main = "Distribution of random variable generated using runif")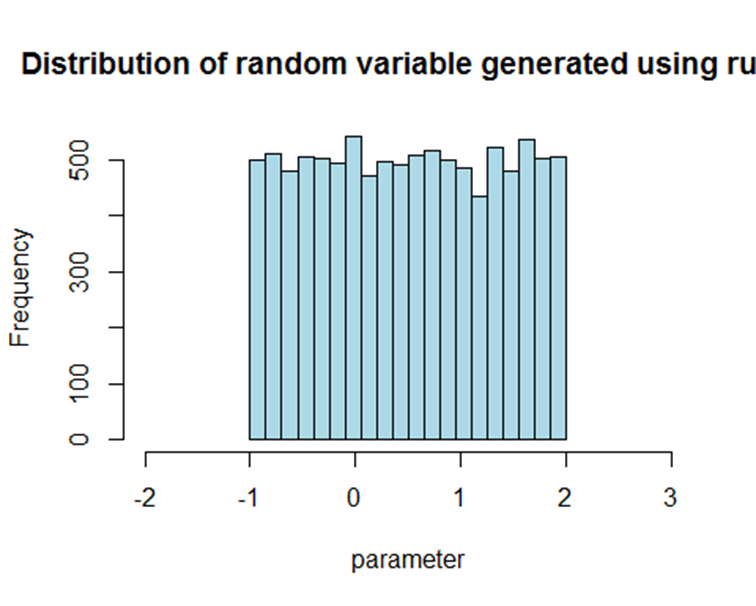
Relative cumulative frequency of uniformly distributed variable
parameter.cut <- cut(parameter, breaks, right = FALSE)
parameter.freq <- table(parameter.cut)
parameter.relfreq <- parameter.freq/n
parameter.cumfreq <- cumsum(parameter.freq)
parameter.cumrelfreq <- parameter.cumfreq / n
parameter.cumrelfreq.0 <- c(0, parameter.cumrelfreq)Plotting Relative Cumulative Distribution of uniformly distributed random variable
plot(parameter.cumrelfreq)
lines(parameter.cumrelfreq)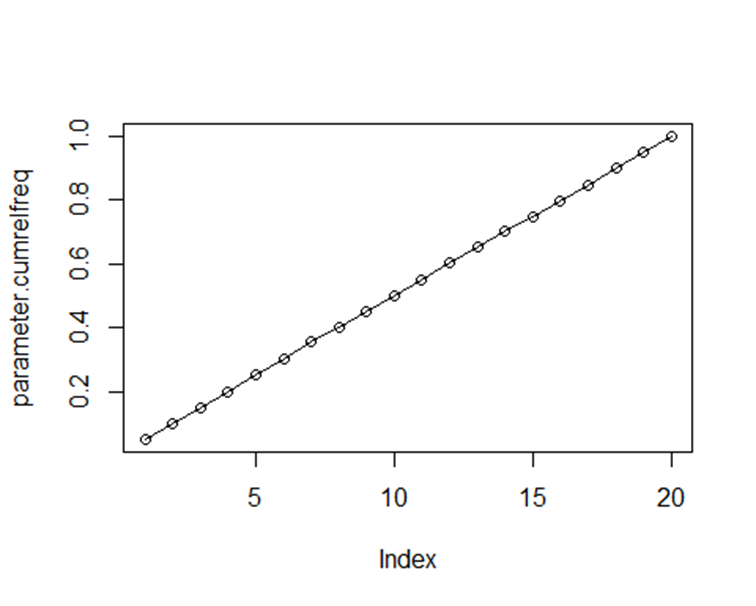
When enough values of random variable are generated, the distribution starts resembling uniform distribution.
Problem 5:
Generating 100×40 matrix
matrix <- replicate(40, runif(100,min,max))Preparation for plotting (x,y1) and (x,y2)
y1 <- matrix[,1]
y2 <- matrix[,2]
y1.cut <- cut(y1, breaks, right = FALSE)
y1.freq <- table(y1.cut)
y1.relfreq <- y1.freq/100
y1data <- data.frame(distribution = y1.relfreq, variable = "y1")
y1data <- y1data %>% select(-distribution.y1.cut)
parameterdata <- data.frame(distribution = parameter.relfreq, variable = "parameter")
parameterdata <- parameterdata %>% select(-distribution.parameter.cut)
y2.cut <- cut(y2, breaks, right = FALSE)
y2.freq <- table(y2.cut)
y2.relfreq <- y2.freq/100
y2data <- data.frame(distribution = y2.relfreq, variable = "y2")
y2data <- y2data %>% select(-distribution.y2.cut)
data <- bind_rows(parameterdata,y1data,y2data)x <- seq(min, max, (max-min)/19)
X <- c(x,x,x)
X <- as.data.frame(X)
data1 <- bind_cols(data, X)Plotting (x,y1)data1 %>%
filter(variable == c("y1", "parameter")) %>%
ggplot() +
geom_line(aes(x = X , y = distribution.Freq, col = variable), size = 1) +
ggtitle("Comparing Relative Distribution of y1 and parameter") +
ylab("Relative Frequency") +
xlab("")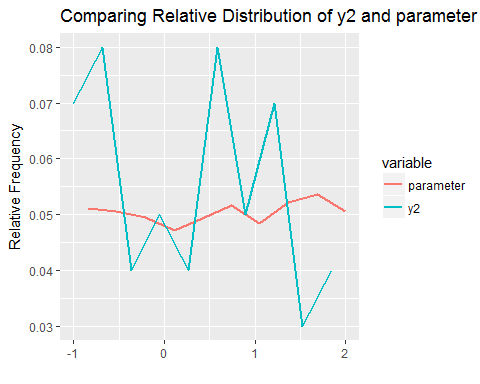
Plotting (x,y2)
data1 %>%
filter(variable == c("y2", "parameter")) %>%
ggplot() +
geom_line(aes(x = X , y = distribution.Freq, col = variable), size = 1) +
ggtitle("Comparing Relative Distribution of y2 and parameter") +
ylab("Relative Frequency") +
xlab("")
Problem 6: Gaussian Curve
summation <- rowSums(matrix)
matrix1 <- cbind(matrix, summation)
normal <- matrix1[,41]
hist(normal,
main = "Plotting summation of Columns",
col = "light blue")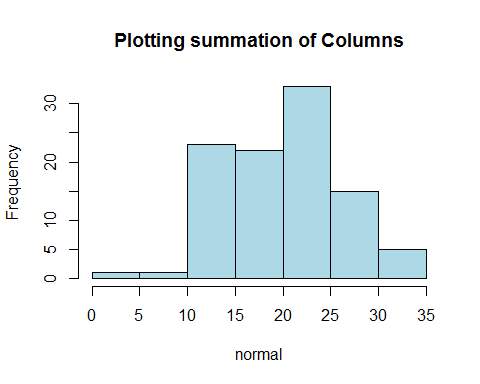
It approximates normal distribution